Introduction

Over the past few decades, quantum computing has emerged as one of the most exciting new technologies. Quantum computers could potentially revolutionize many fields, such as chemistry and cryptography. To reach the capability of efficiently solving real-life problems, some characteristics of quantum computers need to be studied further. With the development of quantum computers still in progress, classical simulation of quantum circuits has proven to be an efficient way to study quantum computing and quantum information.

This article presents Qelvin, a single CPU state vector simulator for study and design of quantum circuits and quantum algorithms. This article discusses the logic, implementation and performance of the simulator.

Background

Universality

A set of quantum gates is said to be universal if any arbitrary quantum circuit can be constructed by only applying the gates in the set. One of these sets consists of general single-qubit and controlled two-qubit unitary gates. [1]

The set of gates implemented in Qelvin includes a single-qubit Hadamard

\[H=\frac{1}{\sqrt{2}}\begin{bmatrix}1 & 1 \\ 1 & -1\end{bmatrix},\]

Pauli gates

\[X=\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix},~Y=\begin{bmatrix}0 & -i \\ i & 0\end{bmatrix},~Z=\begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix},\]

phase shift

\[P(\theta)=\begin{bmatrix}1 & 0 \\ 0 & e^{i\theta}\end{bmatrix},\]

and a general unitary gate

\[U=\begin{bmatrix} u_{11} & u_{12} \\ u_{21} & u_{22} \end{bmatrix}.\]

Controlled two-qubit $X$, $Y$, $Z$, $P(\theta)$ and $U$ gates were also implemented.

Pure states

A $N$ qubit quantum system can be described with a $2^N\times2^N$ density matrix $\rho$. In state vector simulations, a $N$ qubit quantum system is assumed to be in a pure state, enabling all information about the state to be stored in a $2^N$ state vector, significantly reducing the memory required
for the simulation. [1]

Implementation

The techniques used in Qelvin were first introduced in an article about qHiPSTER, the Quantum High Performance Software Testing environment [2]. Rust was the programming language of choice. Rayon was used for parallelization and PyO3 was used to implement Python bindings [3] [4].

State vector

The state vector used in a $N$-qubit system consists of $2^N$ complex numbers. A complex number consists of two $64$ bit double precision floating point numbers that correspond to real and imaginary parts. The total memory required to store the state of the system is thus $2^N\times2\times64$ bits.

Gate application

Let us consider the case where a single-qubit gate $U$ is applied to the $t$:th qubit. The gate needs to be applied to every single state that has the form \(\alpha|b_1b_2...b_{t-1}0b_{t+1}...b_{N}\rangle+\beta|b_1b_2...b_{t-1}1b_{t+1}...b_{N}\rangle,\)

where $b_i\in\{0, 1\}$, $i\neq t$. The difference between the indexes of the two state vectors $b_1b_2…b_{t-1}0b_{t+1}…b_{N}$ and $b_1b_2…b_{t-1}1b_{t+1}…b_{N}$ is $t$. With this information we can form a gate application algorithm:

for g=0; g<2^N; g += 2^(t+1):
    for i=g; i < g+2^t; i++:
        j = i + 2^t
        states[i] = u_11*states[i] + u_12*states[j]
        states[j] = u_21*states[i] + u_22*states[j]

The algorithm can be made suitable for two-qubit controlled $U$ gate by simply adding a conditional statements that checks whether t:th bit of i and/or j equal to one before updating the value in the state vector. This algorithm can be applied to all the gates in our set of gates discussed earlier by simply changing u_11, u_12, u_21 and u_22 to matrix elements corresponding to the gate of choice.

Optimizations

Parallel iteration

Note that the iterations of the innermost loop of the gate application algorithm do not depend on each other making the outer loops parallelizable. In Qelvin states are grouped into chunks each consisting of $2^{t+1}$ adjacent states. Gate application for each chunk is computed in parallel.

Vector instructions

Vector instructions were used to optimize the innermost loop of the gate application algorithm. The innermost loop has four complex multiplications and two complex additions equaling to $4\cdot6+2\cdot2=28$ double precision arithmetic operations done sequentially. By using SIMD (single instruction, multiple data) instructions it is possible to process four double precision floating point numbers simultaneously in parallel improving the throughput of the gate application algorithm. Optimizations related to vector instructions were targeted for CPUs with x86 architecture and AVX and FMA support.

Results

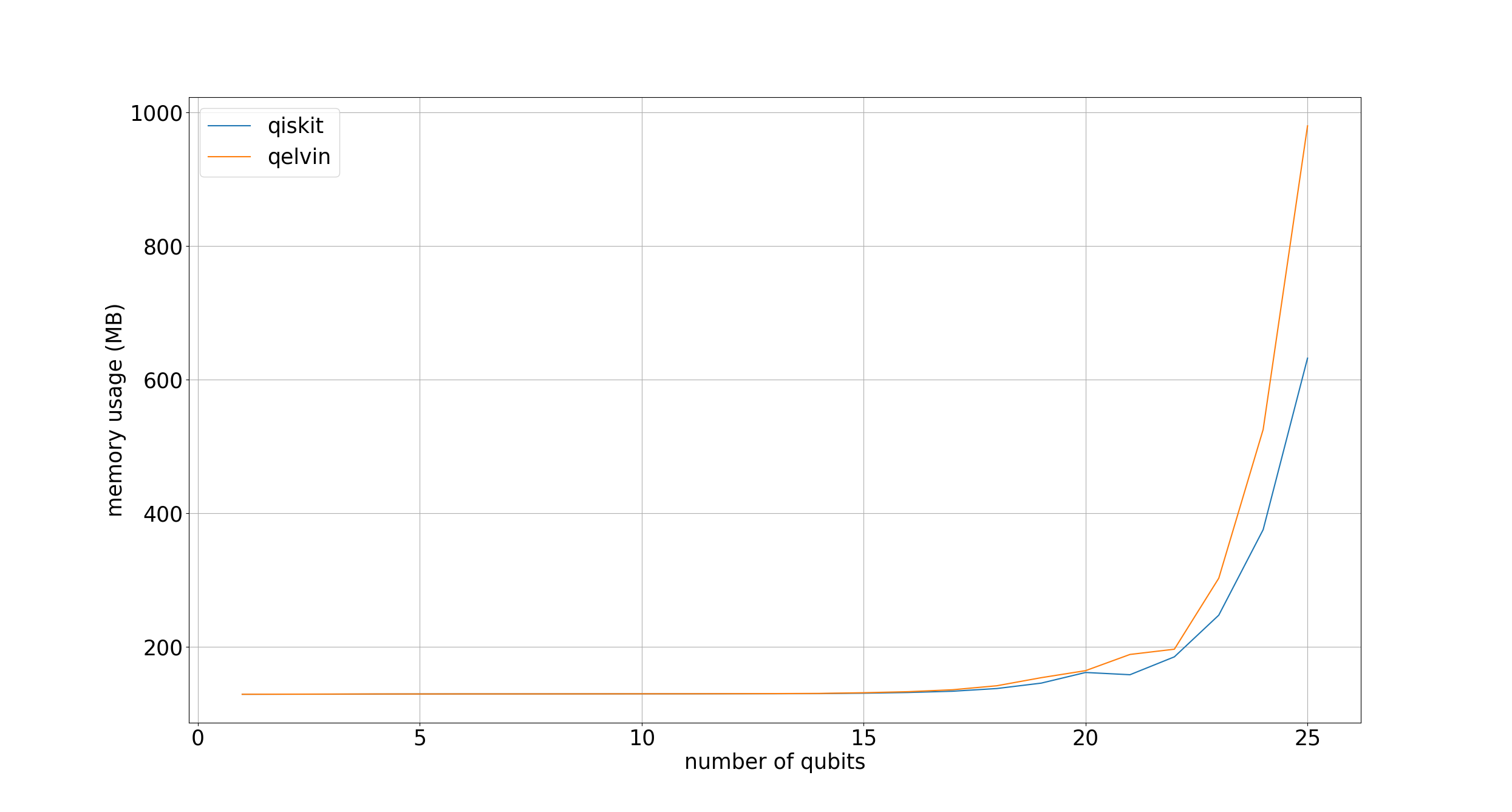
The performance of Qelvin was evaluated by computing the Quantum Fourier Transform for circuits with different number of qubits and benchmarking it against Qiskit [5]. The CPU used in benchmarking was Intel® Core™ i7-8650U. The execution time and memory usage benchmarks are shown in the figures below.

The execution time of Qelvin is slightly shorter compared to Qiskit whereas the memory usage of Qelvin increases faster compared to Qiskit as the number of qubits increases, which is expected since no memory optimizations had not been considered when implementing Qelvin. Qelvin was implemented with specific architecture in mind which may cause less overhead and play a part in the difference in execution time.

Performance of QFT on different number of qubits
Memory usage when computing QFT for systems with different number of qubits

Conclusion

A state vector simulator Qelvin, targeted for single CPU machines, was implemented and benchmarked against an industry-standard software. Qelvin proved to be on par with its counter part in execution time measurements. Lack of memory usage optimizations made Qelvin perform slightly below par in memory usage benchmarks.

Possible future directions for Qelvin involve memory optimization, GPU implementation for the gate application algorithm and usage of multiple CPUs. The source code of Qelvin can be found online [6].

References

  1. Smelyanskiy, M., Sawaya, N. P. D., & Aspuru-Guzik, A. (2016). qHiPSTER: The Quantum High Performance Software Testing Environment.
  2. Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press.
  3. Rayon Project and Contributors. Rayon. https://github.com/rayon-rs/rayon
  4. PyO3 Project and Contributors. PyO3. https://github.com/PyO3/pyo3
  5. Qiskit contributors. (2023). Qiskit: An Open-source Framework for Quantum Computing. https://doi.org/10.5281/zenodo.2573505
  6. Näsman D. Qelvin. https://github.com/dannasman/qelvin